I have been using tensorflow for some examples in this blog. Building a sequential model and evaluating some metrics was easy. But when I wanted to do a little bit more (for example image data set augmentation) I got really stuck.
This blog post is a collection of toy examples I made from scratch with tensorflow in order to get a better understanding.
The following video is a good introduction to tensorflow (although it is pretty old):
The computational graph: Session and constant
A programmer can construct a computational graph with tensorflow. It does not contain data or is evaluated directly. For this reason we need sessions where we can feed data in and fetch results out.
import tensorflow as tf
For jupyter notebook there is an interactive session:
sess = tf.InteractiveSession()
In real programs we use:
with tf.Session() as sess:
# Let us build a simple mathematical expression
# (13 * 13) - (12 * 12) - (11 * 11)
a = tf.constant(11)
b = tf.constant(12)
c = tf.constant(13)
result = a*a - b*b - c*c
Obviously we would like to read the result but one might be surprised to see that no value is returned. Instead we obtain a node from the computational graph…
result.eval() in an interactive session or sess.run([result]) delivers what we expect!
Placeholders
But this is kind of cheap. A calculation formed of constant values. What about something like \(f(x) = x^2 + 4x + 8\)?
For this we use placeholders. We define their size and datatype and feed them into the eval or run command.
# The placeholder for the parameter
x = tf.placeholder(tf.float32)
# the function
f = x*x + 4*x + 8
# f(x=0) in interactive session
f.eval(feed_dict={x:0})
Okay interesting. We can build things with this. Let’s imagine we have ball with mass m and we want to know the potential energy it has (m * g * h).
# the mass m in kilogram
m = tf.placeholder(tf.float32)
# the height h in meters
h = tf.placeholder(tf.float32)
# gravitational constant of the earth
g = tf.constant(9.81)
# potential energy
e_pot = m * g * h
# Now let's say we want to lift the ball with a
# mass of 400g from the ground to a height of
# 1.8 meters. How much is the energy difference?
difference = e_pot.eval(feed_dict={m:0.4, h:1.8}) - e_pot.eval(feed_dict={m:0.4, h:0})
print("{} Joule(?)".format(difference))
Adding state to the graph
Suppose we have a dynamical system like a simulation of a swing or of the populations in a forest. These systems have something called a state. In programming we represent and manipulate this with variables. This concept also exists for tensorflow.
The following example calculates n fibonacci numbers in a non-recursive way. So the same graph is called n times and the variables’ contents change for every iteration.
It is important to say that the manipulation of variables (reading and writing) justifies the need for another new thing called control dependencies. One can use them to assure the execution of a sequence in its correct order.
import tensorflow as tf
# Make the graph empty
tf.reset_default_graph()
# Create two variables for the fibonacci numbers and one for the swap
number_one = tf.get_variable("number_1", initializer=tf.constant([0], dtype=tf.int64))
number_two = tf.get_variable("number_2", initializer=tf.constant([1], dtype=tf.int64))
# Variable for the swapping
number_tmp = tf.get_variable("number_3", initializer=tf.constant([0], dtype=tf.int64))
# Operation to temporarily store one of the numbers
store_tmp = tf.assign(number_tmp, number_two)
# First store one of the numbers
with tf.control_dependencies([store_tmp]):
sum_of_both = tf.add(number_one, number_two)
# then calculate the sum
with tf.control_dependencies([sum_of_both]):
# and over finally overwrite the variables' values
assign_new_number_one = tf.assign(number_one, number_tmp)
assign_new_number_two = tf.assign(number_two, sum_of_both)
# group the last assignments -> only call this later
next_fib = tf.group([assign_new_number_one, assign_new_number_two])
# Here we store the fibonacci numbers
numbers = []
# How many numbers do we want?
n = 100
with tf.Session() as sess:
# Store the graph
file_writer = tf.summary.FileWriter('tf_logs', sess.graph)
# Init vars
sess.run(tf.global_variables_initializer())
for _ in range(n):
# Run the group which has to execute its control dependencies first
sess.run([next_fib])
# store the variables
x = [number_one.read_value().eval(),
number_two.read_value().eval(),
number_tmp.read_value().eval()
]
numbers.append(x)
# Extract only the fibonacci numbers with numpy
import numpy as np
fibs = np.asarray(numbers)[:, 1].flatten()
print(fibs)
The assignment file_writer = tf.summary.FileWriter('tf_logs', sess.graph) writes the computational graph to disk and we can visualize it with tensorboard:
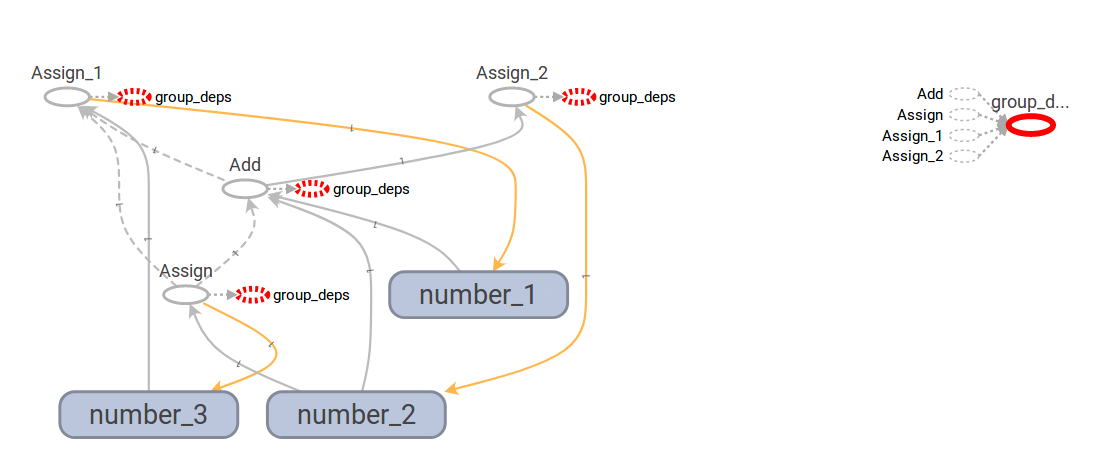
I am not sure but I think: The yellow line shows a connection where the data could have been manipulated, the solid grey line where data flows without manipulation and the dashed lines are control flow operations.
The blue rectangles with round corners are variables. The white ellipsis with grey border is an operation and the ellipsis with red dashed border is the grouping.
My intuition on how to read this graph is:
- Find operations which do not have incoming dashed grey lines (control flow) and no incoming lines from such nodes (this excludes “Assign_2”). They are free to be evaluated without prerequisites. -> “Assign”
- After “Assign” is done it is the turn of “Add” and then “Assign_1” and “Assign_2” could potentially be executed in parallel
Finding primes with a while loop
The following program uses a while loop to tell whether a number is prime. Tensorflow can help to parallelize while loops “automagically”. Imagine you could write loops that can be placed on GPUs instantaneously…
Tensorflow’s explains how the tf.while_loop works: White paper tensorflow control flow.
The following image shows the basic components which were added in order to achieve the control flow (screenshot taken from paper).
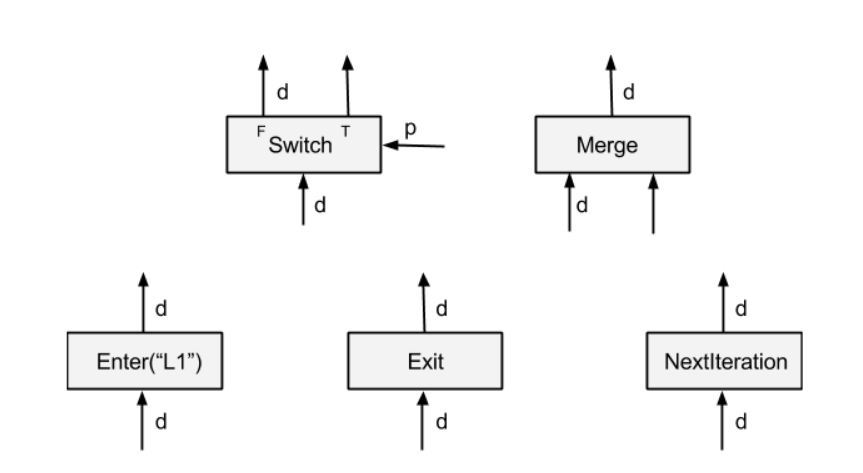
From the paper:
Enter(name): An Enter operator forwards its input to the execution frame that is uniquely identified by the given name. This Enter op is used to pass a tensor in one execution frame to a child execution frame. There can be multiple Enter ops to the same child execution frame, each making a tensor available (asynchronously) in that child execution frame. An Enter is enabled for execution when its input is available. A new execution frame is instantiated in the TensorFlow runtime when the first Enter op to that frame is executed.
Exit: An Exit operator forwards a value from an execution frame to its parent execution frame. This Exit op is used to return a tensor computed in a child execution frame back to its parent frame. There can be multiple Exit ops to the parent frame, each asynchronously passing a tensor back to the parent frame. An Exit is enabled when its input is available.
NextIteration: A NextIteration operator forwards its input to the next iteration in the current execution frame. The TensorFlow runtime keeps track of iterations in an execution frame. Any op executed in an execution frame has a unique iteration id, which allows us to uniquely identify different invocations of the same op in an iterative computation. Note that there can be multiple NextIteration ops in an execution frame. The TensorFlow runtime starts iteration N+1 when the first NextIteration op is executed at iteration N. As more tensors enter an iteration by executing NextIteration ops, more ops in that iteration will be ready for execution. A NextIteration is enabled when its input is available.
The prime search code:
# --------------------------
# PRIME CHECKING TENSORFLOW
# --------------------------
import tensorflow as tf
# The number at the bench
number = tf.placeholder(tf.float32, name="number")
# Possible divisors which are increased [1...number-1]
i = tf.get_variable("i", dtype=tf.float32, initializer=tf.constant(2.0))
# Store the result if the calculation gets through
is_prime = tf.get_variable("is_prime", dtype=tf.bool, initializer=tf.constant(True))
# The "stop criterion" for the while-loop
def condition(number, i, is_prime):
return tf.logical_and(
tf.less(i, number),
tf.equal(is_prime, tf.constant(True)),
name="and"
)
# The code that gets executed for every iteration
def body(number, i, is_prime):
# remainder = number % i
remainder = tf.floormod(number, i, name="remainder")
# not_divisable = remainder != 0
not_divisable = tf.not_equal(remainder, tf.constant(0.0), name="not_divisable")
# is_prime AND not_divisable
result_is_prime = tf.logical_and(is_prime, not_divisable)
# This line is necessary because the shape of result_is_prime is not fixed
result_is_prime.set_shape(is_prime.shape)
# A print statement in tensorflow has to be a proper node
# or else it will not get executed
result_is_prime2 = tf.Print(result_is_prime,
[number, i, remainder, not_divisable, result_is_prime],
name="remainder_before")
# The body function has to return the same amount of tensors as it got
# via parameters.
return number, tf.add(i, tf.constant(1.0)), result_is_prime2
# The main operation is the while loop
search_op = tf.while_loop(
condition,
body,
[number, i, is_prime]
)
with tf.Session() as sess:
# Store the graph
file_writer = tf.summary.FileWriter('tf_logs', sess.graph)
# search the number 1 to 100
for x in range(1, 100):
# Init vars
sess.run(tf.global_variables_initializer())
# Run the session and get the last return values of the loop
_, _, x_is_prime = sess.run([search_op], feed_dict={number: x})[0]
if x_is_prime:
print("{} is prime".format(x))
else:
print(x)
The collapsed computational graph looks far too simple:
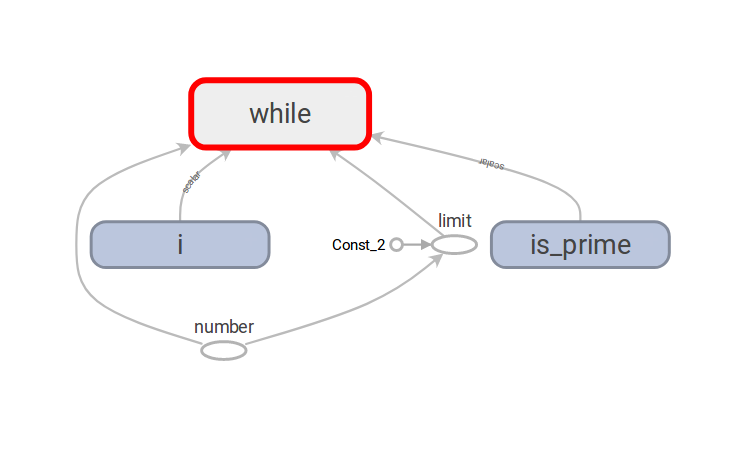
When unfolding the while block, we see a lot of operations which we did not explicitly mention in the python code.
Every variable that is passed in to the functions (condition and body) run through an “Enter” node.
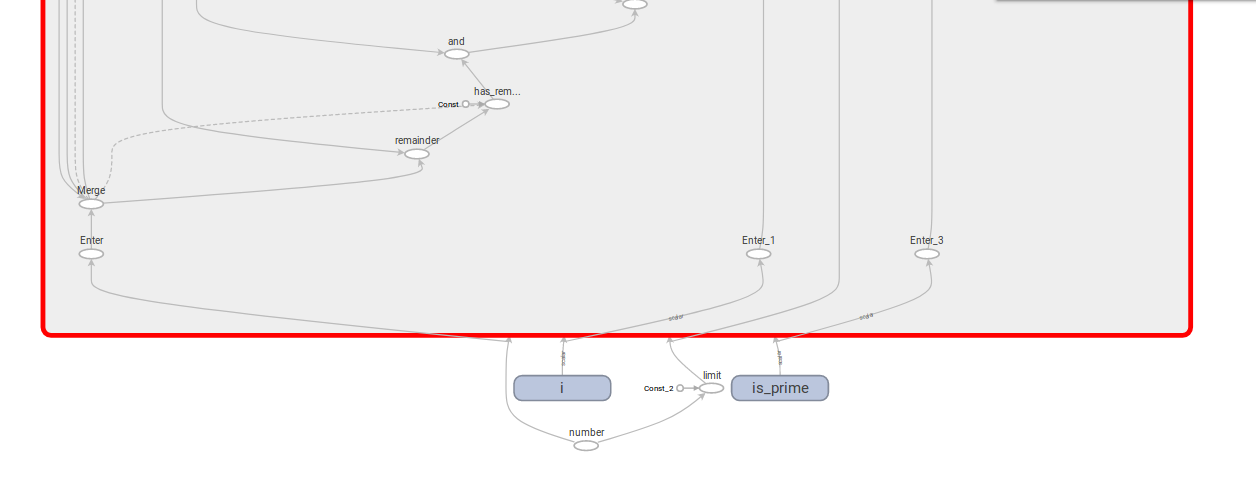
All of the python code which was written to manipulate the variables was translated into the graph. I find this really impressing because I did not feel really restricted when writing the condition and body for the loop.
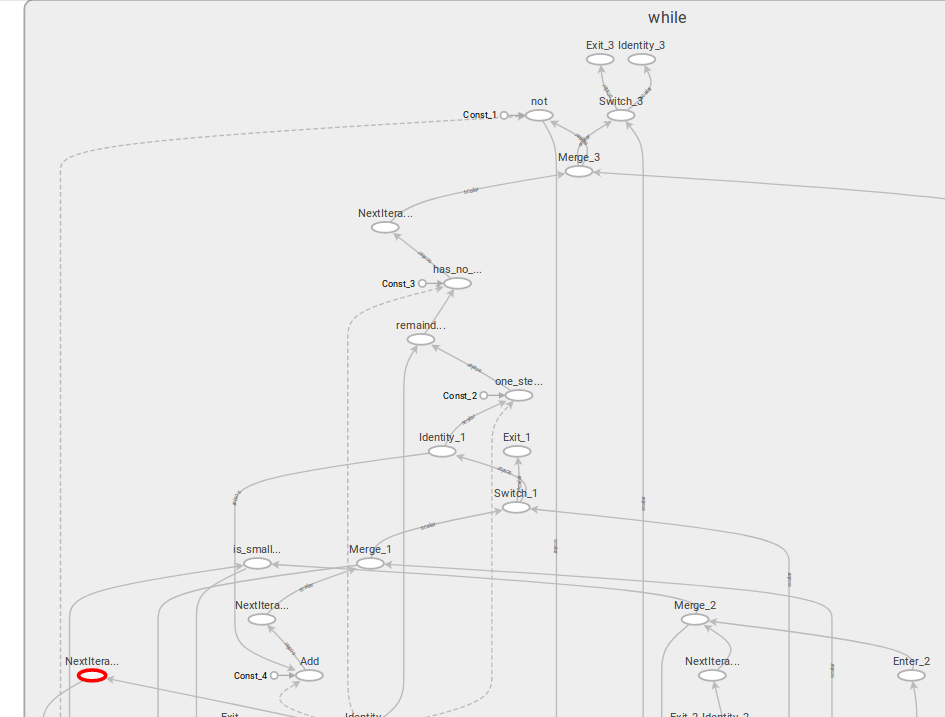
The big benefit of this (telling from what I read on the web) is that it supports auto differentiation. So one could write a loop to solve some problem and end-to-end learning could still be possible.
Image manipulation
Now I have made a toy example that:
- Reads all images from a list of filenames
- Makes them look old
- Stores the images back to disk
# This tensorflow program makes an image look old and sepia style
import tensorflow as tf
import numpy as np
import scipy.stats as st
# The target dimensions of the image
W = 600
H = 400
def _parse_function(filename, intensity):
"""Reads an image from a file, decodes it into a dense tensor"""
image_string = tf.read_file(filename)
image_decoded = tf.image.decode_jpeg(image_string)
image_resized = tf.image.resize_images(image_decoded, [H, W])
return image_resized, intensity, filename
def noisening(image, intensity, filename):
"""Adds random noise to the image"""
noise = tf.random_uniform([H, W, 3], minval=1, maxval=100, dtype=tf.int32)
image = tf.cast(image, tf.int32)
image = image + noise
# all pixels between 1, 255
image = tf.clip_by_value(image, 1, 255)
image = tf.cast(image, tf.uint8)
return image, intensity, filename
def sepia(image, intensity, filename):
"""Changes the colors of the image to sepia"""
image = tf.cast(image, tf.float32)
# Extract the color channel
red = image[:, :, 0]
green = image[:, :, 1]
blue = image[:, :, 2]
# Apply a color matrix from
# https://www.techrepublic.com/blog/how-do-i/how-do-i-convert-images-to-grayscale-and-sepia-tone-using-c/
output_red = red * 0.393 + green * 0.769 + blue * 0.189
output_green = red * 0.349 + green * 0.686 + blue * 0.168
output_blue = red * 0.272 + green * 0.534 + blue * 0.131
# bring color channels back together
image = tf.stack([output_red, output_green, output_blue], axis=-1)
image = tf.cast(image, tf.uint8)
return image, intensity, filename
def gkern(kernlen=21, nsig=3):
"""Returns a 2D Gaussian kernel array."""
interval = (2*nsig+1.)/(kernlen)
x = np.linspace(-nsig-interval/2., nsig+interval/2., kernlen+1)
kern1d = np.diff(st.norm.cdf(x))
kernel_raw = np.sqrt(np.outer(kern1d, kern1d))
kernel = kernel_raw/kernel_raw.sum()
return kernel
def blur(image, intensity, filename):
"""Blur the image with gaussian"""
# Make Gaussian Kernel with desired specs.
gauss_kernel = gkern(10, nsig=3)
# Expand dimensions of `gauss_kernel` for `tf.nn.conv2d` signature.
gauss_kernel = gauss_kernel[:, :, tf.newaxis, tf.newaxis]
image = tf.cast(image, tf.float32)
# Convolution only works on 4d tensor
batch = image[:, :, :, tf.newaxis]
# Convolve.
batch = tf.nn.conv2d(batch, gauss_kernel, strides=[1, 1, 1, 1], padding="SAME")
image = tf.squeeze(batch)
image = tf.cast(image, tf.uint8)
return image, intensity, filename
def frame(image, intensity, filename):
"""Add a black frame to the image"""
width = 20
half = 10
image = tf.image.pad_to_bounding_box(
image,
half,
half,
H + width,
W + width
)
return image, intensity, filename
# A vector of filenames.
filenames = tf.constant(["1.JPG",
"2.JPG"])
# `intensities[i]` is the intensity for the image in `filenames[i].
# 0 to 100
intensities = tf.constant([50, 100])
# Create a new dataset zip(filenames, intensities)
dataset = tf.data.Dataset.from_tensor_slices((filenames, intensities))
# Pipeline for every image
dataset = dataset.map(_parse_function)
dataset = dataset.map(noisening)
dataset = dataset.map(blur)
dataset = dataset.map(sepia)
dataset = dataset.map(frame)
# Get an iterator without placeholders that can be used once
iterator = dataset.make_one_shot_iterator()
# The nodes to work with in the graph
image, intensity, filename = iterator.get_next()
# Store the processed image
new_filename = filename + ".new.JPG"
image_string = tf.image.encode_jpeg(image)
write_op = tf.write_file(new_filename, image_string)
with tf.Session() as sess:
file_writer = tf.summary.FileWriter('tf_logs', sess.graph)
sess.run(tf.global_variables_initializer())
for i in range(2):
sess.run(write_op)
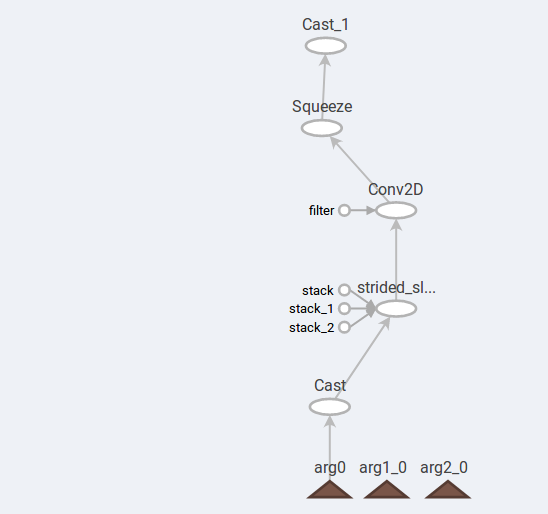
Note the use of tf.data.Dataset and that the tf.write_file operation could not be part of the .map function because it would not get called due to no other operation depending on it.
The main graph contains the operations outside of the functions only.
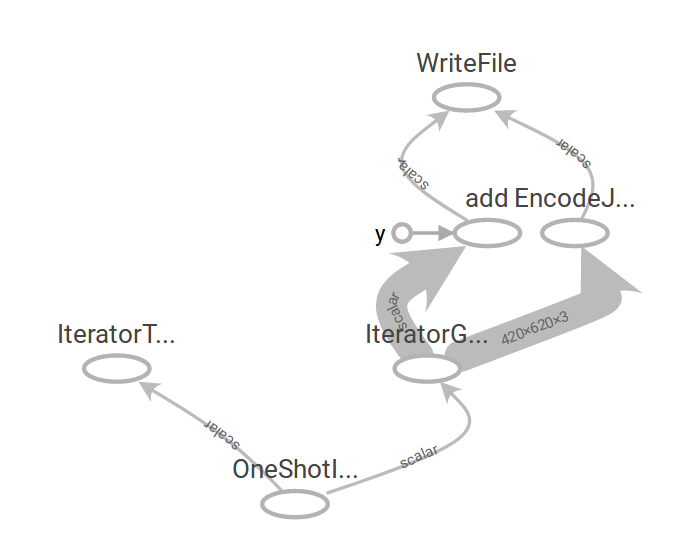
Opening for example the blur function shows us the bigger parts of the computational graph.