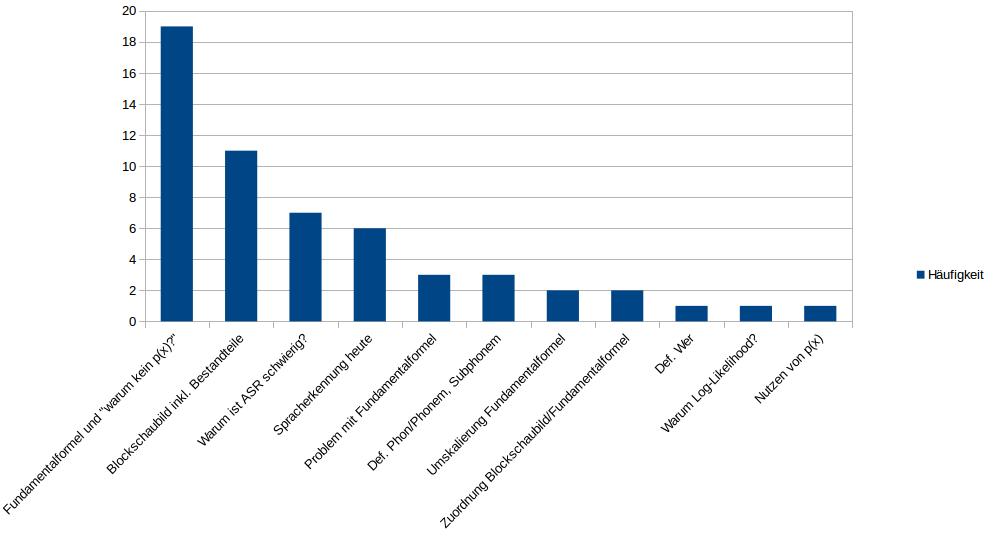
A fellow student counted the most frequent exam questions for the course “Grundlagen der Automatischen Spracherkennung” as I am preparing for the oral exam I thought that a visualization of this would be cool.
About the course
I attended the course in the winter semester 2018/2019 by Dr. Stüker. The recordings from the year before are available on Youtube; he told us that the contents are still up-to-date.
The general task is called continuous speech recognition. ASR: To transform a recording of human speech automatically into a string of word that can be processed by a computer.
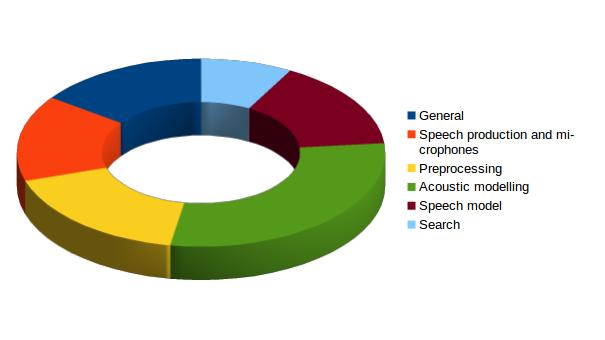
These were the topics with their counts from which the questions came:
- General: 56
- Speech production and microphones: 55
- Preprocessing: 65
- Acoustic modelling: 109
- Speech model: 57
- Search: 30
General questions
What is the “Fundamental Formel”?
\[\hat{W} = arg_{W} max P(W|X) \overset{\text{Bayes}}{\underset{\text{}}{=}} arg_{W} max \frac{P(X|W) P(W)}{P(X)} \overset{\text{maxim.}}{\underset{\text{}}{=}} arg_{W} max P(X|W) P(W)\]P(W|X) is the a-posteriori, P(X|W) the likelhood which we call the acoustic model in ASR, P(W) and P(X) are both a-prioris where P(W) is called the language model and P(X) is the evidence of the data which falls away because most of the time we decide to maximize my maximizing the enumerator. W is a sequence of words. arg max is called the “search” or “decoding”.
Draw the block diagram!
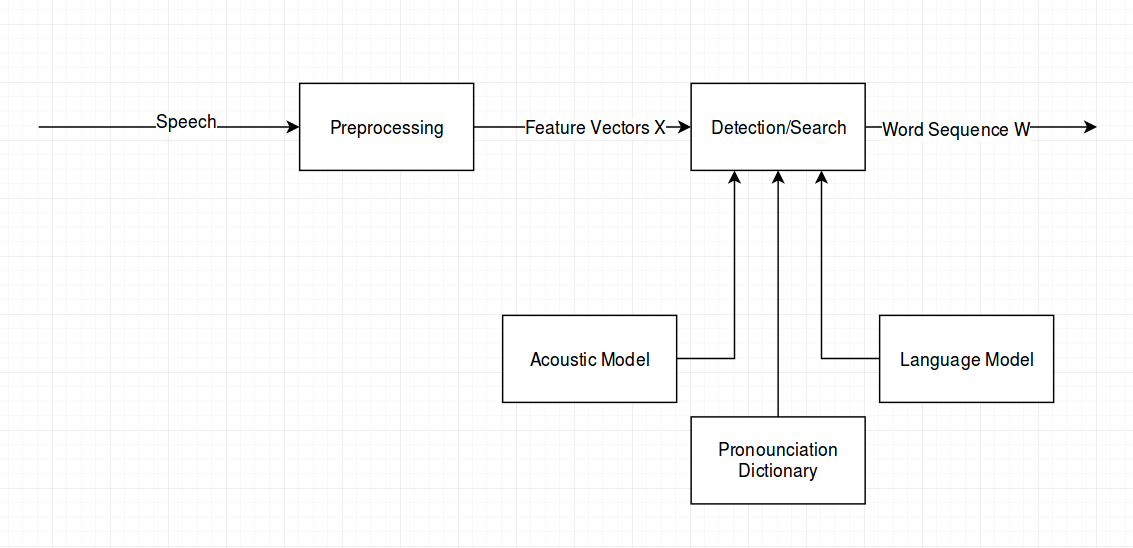
- Speech: Recorded via microphone
- Preprocessing: Usually MFCC and dynamic features
- Feature vectores: 42 dimensions for every frame
- Detection: For example a multipass search with (1) search space activation with viterbi decoding, (2) more detailed search with stack decoding to generate n-best list and (3) find the best hypothesis by search the word graph generated by n-best list
- Acoustic model: Evaluate the likelihood of a word sequence by calculating \(P(X\|W)\) with HMM+GMM or HMM+ANN (goes down to sub-triphone level)
- Pronunciation dictionary: With the help of this any word can be split into phonemes or smaller linguistic units in order to detect words that were not seen during training
- Language model: Calculate the probability of the word sequence for example with a n-gram model
Why is ASR difficult? Because of the variability in the signal, in the acoustic and in the speech. In the signal because of microphones, reverberations of the room… In the acoustics because of the velocity, volume or voice of a person. In the speech: Which words, regional differences of languages, dialects…
Speech recognition today? Because of the variability we treat speech partially as a random process and we use statistical speech recognition to solve for this. We use graphical models like HMMs to combine phonetic a-priori knowledge with training data. At its heart we treat speech recognition as a classification problem with the word error rate as performance measure. Here comes the fundamental formula into play.
What kind of flaw is in the fundamental formula? The language model P(W) is a discrete probability distribution and the acoustic model P(X|W) is a continuous probability distribution in the case of HMM+GMM. This results in a variance problem where the language model brings in too much probability mass. Therefore we modify the formula a little bit:
\[P(W\|X) = P(X\|W) * P(W)^z / P(X)\]with z <= 1.0 cross validated
And there is also another problem. Long word sequences are less probable than short ones in most language models therefore we can also add a factor that takes this into account.
\[P(W\|X) = P(X\|W) * P(W)^z * q^{|W|} / P(X)\]with q cross validated
Definition phon, phonem and subphonem? A phon is the smallest acoustic unit which can be perceived. A phonem is the smallest acoustic unit which can make a semantic difference between words. A subphonem is a part of a phonem.
Rescaling the fundamental formula? See above
\[P(W|X) = P(X|W) * P(W)^z * q^{|W|} / P(X)\]Definition WER? Word Error Rate:
\[WER = \frac{ \#INS + \#DEL + \#SUB}{\|REF\|}\]Languages that do not split into words are suboptimal for this metric.
Why log likelhood? The log is a strictly monotonic function which results in the fact that the extreme values of the log of a function reside at the same value as the original function. If we only want to find an extreme value we can therefore also find the extreme value of the log function. The log comes in especially handy for two reasons. Avoid the evaluations of e-functions and if for calculations that become numerically unstable.
What is the use of p(x)? We call p(x) the evidence of the data. It is used for discriminative training which has the target to maximize the distance between the correct word sequence and the incorrect ones. The same holds for Maximum Mutual Information Estimation (MMIE).
We can calculate p(x) by marginalizing over all possible word sequences. This is not feasible in practice. As a substitute we can use a n-best list.
Note
I cut the other (more important) topics because it might not be a good idea to make this information available to the Internet, sorry.