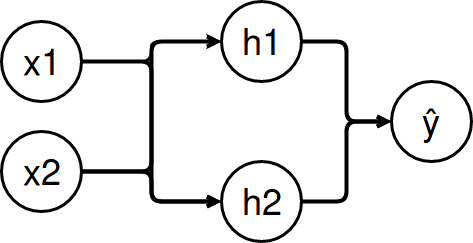
Calculating backpropagation by hand
My last post was about a feed forward net. I did not explain where the weights in the network came from.
This entry explains back propagation and contains a calculation for the example from the last post which was about approximating the XOR function.
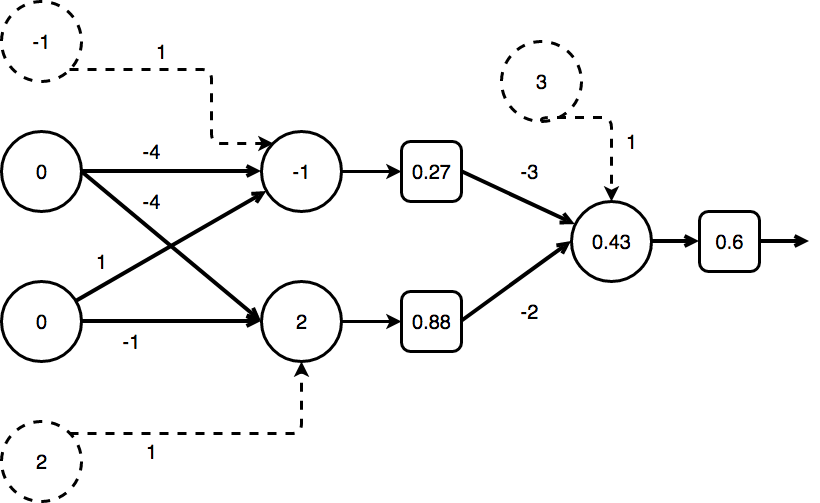
Initial values
Let’s initialize the values of both weight matrices and biases with random numbers from [-4, 4]\{0}:
And let the learning rate be \(\alpha = 1\) .
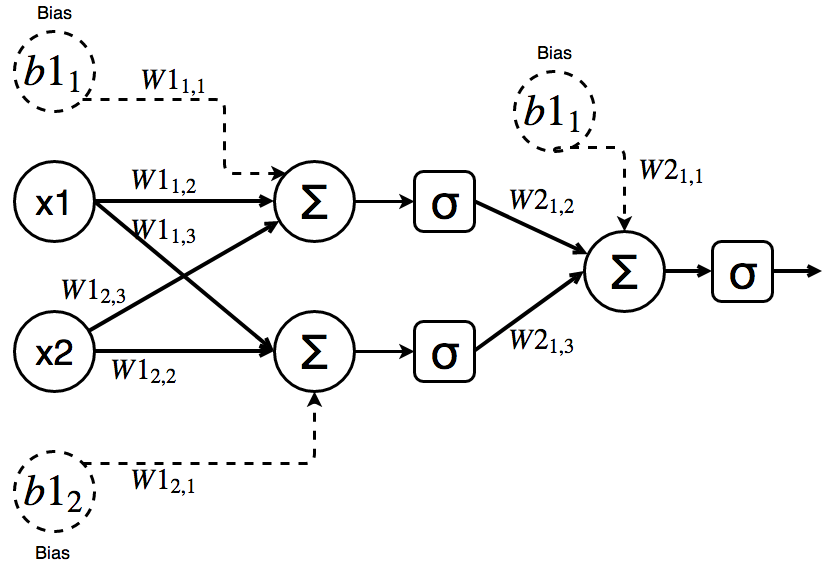
Forward propagation
Backpropagation is an online algorithm which means “one example at a time”. The first step is to calculate the prediction for given x-values and calculate the error using the attached label.
| x XOR y | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
For \(x = (0, 0)^T\) the calculation of y is as follows:
\[\sigma (\begin{pmatrix} -3 & -2 \end{pmatrix} * \sigma \bigg( \begin{pmatrix} -4 & -4 \\\ -1 & 1 \end{pmatrix} * \begin{pmatrix}0\\\ 0\end{pmatrix} + \begin{pmatrix}-1\\\ 2\end{pmatrix} \bigg) + \begin{pmatrix}3 \end{pmatrix}) =\] \[\sigma (\begin{pmatrix} -3 & -2 \end{pmatrix} * \begin{pmatrix}0.27 \\\ 0.88 \end{pmatrix} + \begin{pmatrix}3 \end{pmatrix}) =\] \[\sigma ( 0.43 ) = 0.6\]Backward propagation
0 XOR 0 should be 0. We can now calculate the error of the output neuron(s): \(y - ŷ = 0 - 0.6 = -0.6\)
But how do we calculate the error of the hidden units? We don’t have a supervision to directly compare them to something.
The image above shows all of the steps and variables necessary for our XOR neural net. The weights to the biases where ignored so far as they were ones. If we want to change the weight of one bias, we just add the difference to the bias itself.
With the error to the output neuron we can calculate the error of every single neuron that is connected to the output neuron:
Error of hidden neuron h_i:
\[E_{h_{i}} = \frac{\partial E}{\partial h_{i}} = \sum_{j} \sigma ' (y_{i}) * W2_{i,j} \frac{\partial E}{\partial y_{j}}\]- We want to know the error of the neuron to change its value accordingly: \(\frac{\partial E}{\partial h_{i}}\)
- The error of the hidden neuron depends on the neurons that come after it. In this case it is only the output neuron: \(\frac{\partial E}{\partial y_{i}}\)
- The changerate of the output neuron depends on how the hidden neuron is changed: \(\sigma ' (y_{i}) * W2_{i,j}\)
- \(\sum\) and then all of these partial errors to single neurons that come after are summed up to determine how much the single hidden neuron affects the next layer
- The derivative of sigma is \(\sigma ' (x) = e^x \div (1 + e^x)^2\)
Calculate the errors of the hidden layer
The following image contains all the numbers from the feed forward step:
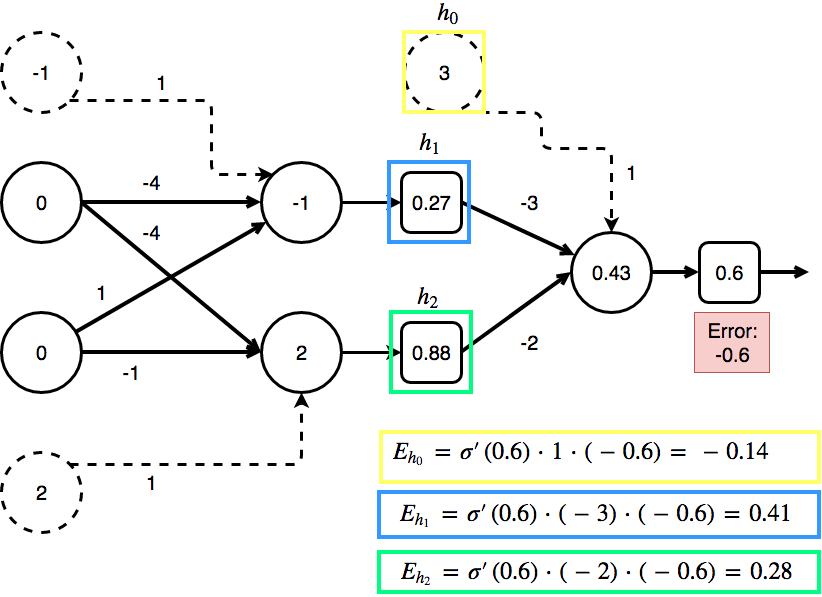
Calculate the errors on weights
Now that we know how to calculate the error on hidden neurons we can calculate the error on weights.
Error on weight w connecting two neurons. h_i from hidden layer h and y_i from output layer y:
\[\frac{\partial E}{\partial w} = \frac{\partial E}{\partial y_i} \sigma ' (y_i) * h_i\]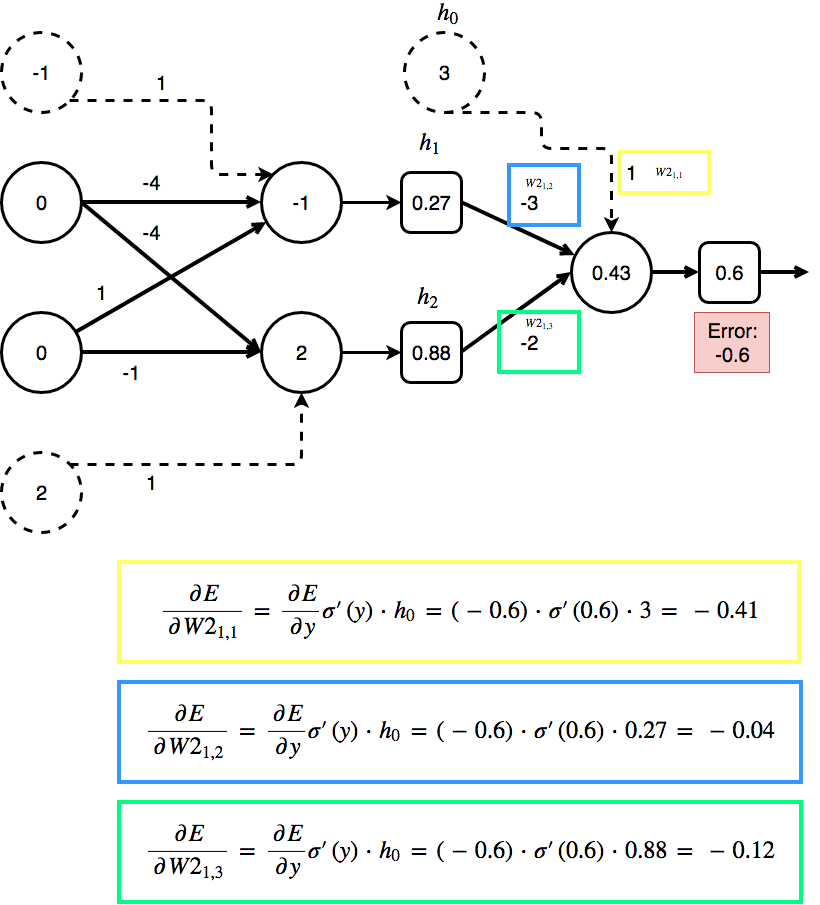
This error (which is the derivative of the error to one neuron) is used to update the weight w:
\[w \leftarrow w - \alpha * \frac{\partial E}{\partial w}\]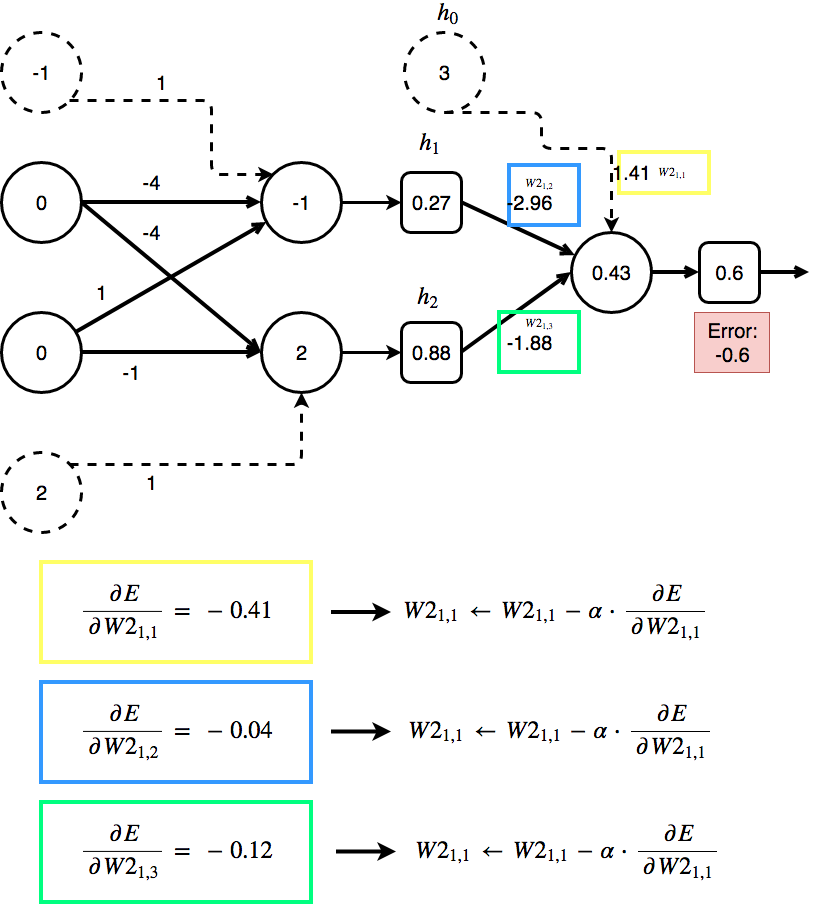
This have been the three important steps of backpropagation:
- Feed forward
- Calculate errors
- Update weights
In the next post I am going to present a small python script to evaluate whether the shown calculations can find a proper approximation to the XOR function.
There are good videos on this topic available: https://www.youtube.com/watch?v=aVId8KMsdUU
https://www.youtube.com/watch?v=zpykfC4VnpM

